In the wake of ever-growing power demands, power systems optimization (PSO) of power grids is crucial for ensuring efficient resource management, sustainability, and energy security.

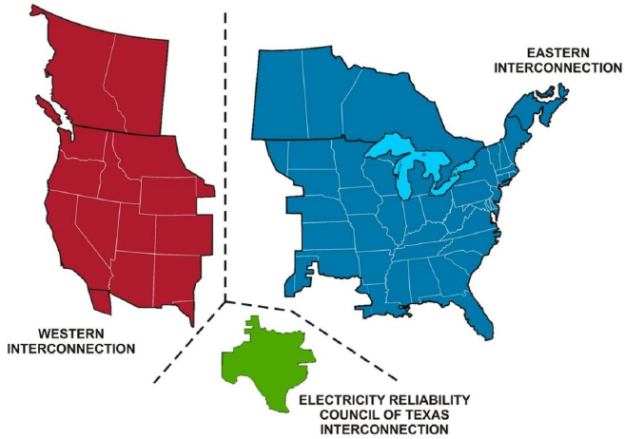
The Eastern Interconnection, a major North American power grid, consists of approximately 70K nodes (Figure 1). Aside from sheer size, optimizing such a grid is complicated by uncertainties such as catastrophic weather events and disruptions in power generation.

PSO typically involves solving large-scale nonlinear optimization problems, such as alternating current optimal power flow (ACOPF) models, often with millions of variables and constraints. Obtaining accurate results in real time is critical for maintaining grid stability and efficiency, but is an incredibly difficult task.

Professor Sungho Shin (MIT), Professor François Pacaud (MINES Paris – PSL), and postdoctoral researcher Alexis Montoison (ANL) have been developing nonlinear optimization algorithms and solvers that use NVIDIA tools to solve large-scale PSO and other complex nonlinear optimization problems.

Their most recent paper, Condensed-space methods for nonlinear programming on GPUs, takes advantage of the NVIDIA cuDSS (Direct Sparse Solver) library and high-memory GPUs like the NVIDIA Grace Hopper Superchip to solve problems at scales never before possible.

Solving nonlinear optimization problems

Nonlinear optimization of large-scale, sparse, constrained problems like PSO is predominantly solved using interior-point methods. Solvers such as IPOPT, KNITRO, and MadNLP iteratively search for solutions by calculating a step direction, which involves solving a sequence of Karush-Kuhn-Tucker (KKT) systems and determining the step size through line-search criteria (Figure 2).

The evaluation of KKT system entries—the derivatives of the objective and constraints—and the numerical solution of the KKT systems are computationally intense and typically delegated to external libraries. Derivative evaluations are handled by algebraic modeling systems with automatic differentiation capabilities (AMPL, Pyomo, or JuMP.jl), while the KKT systems are solved using sparse linear solvers (Pardiso, MUMPS, or HSL).

The primary bottleneck of the interior-point algorithm is solving the KKT systems, which are often large, sparse, and ill-conditioned. Due to the difficulties of designing preconditioners for iterative linear solvers, direct solvers become the tool of choice for obtaining accurate enough solutions of KKT systems.

In traditional implementations, sparse solvers using LBLᵀ factorization, such as the MA27 and MA57 linear solvers from the libHSL collection, are commonly used. While accelerated parallel computing holds great potential for accelerating large-scale optimization, efficient direct sparse solvers for the GPU have been elusive.

Libraries such as NVIDIA cuDSS focus on these sorts of gaps.

Powering large-scale PSO solvers with cuDSS

Efficient GPU implementation of interior-point methods is now available thanks to breakthroughs in the MadNLP program that can make use of the new cuDSS library. MadNLP uses condensed KKT procedures (lifted and hybrid), which reformulate the problem as a sparse positive-definite system instead of the original indefinite system.

cuDSS can then efficiently factorize and solve the condensed KKT system on GPUs, enabling significant performance improvements for large-scale nonlinear optimization.

Sungho, François, and Alexis used these capabilities to develop a comprehensive software suite that runs nonlinear optimization fully on NVIDIA GPUs. This suite includes ExaModels, for algebraic modeling and automatic differentiation, and MadNLP, for implementing interior-point methods with lifted and hybrid KKT system strategies (Figure 2).

This suite of tools produced massive speedups for PSO problems large enough to model the entire Eastern Interconnection, more than 70K nodes and corresponding to a 674K dimensional system. Accelerating the ExaModels, MadNLP, and cuDSS parts of the workflow with an NVIDIA A100 GPU resulted in the first realization of a real-time solution (less than 20 seconds) for problems of this scale. This demonstrates that computational barriers no longer inhibit the practical PSO of the entire Eastern Interconnection.

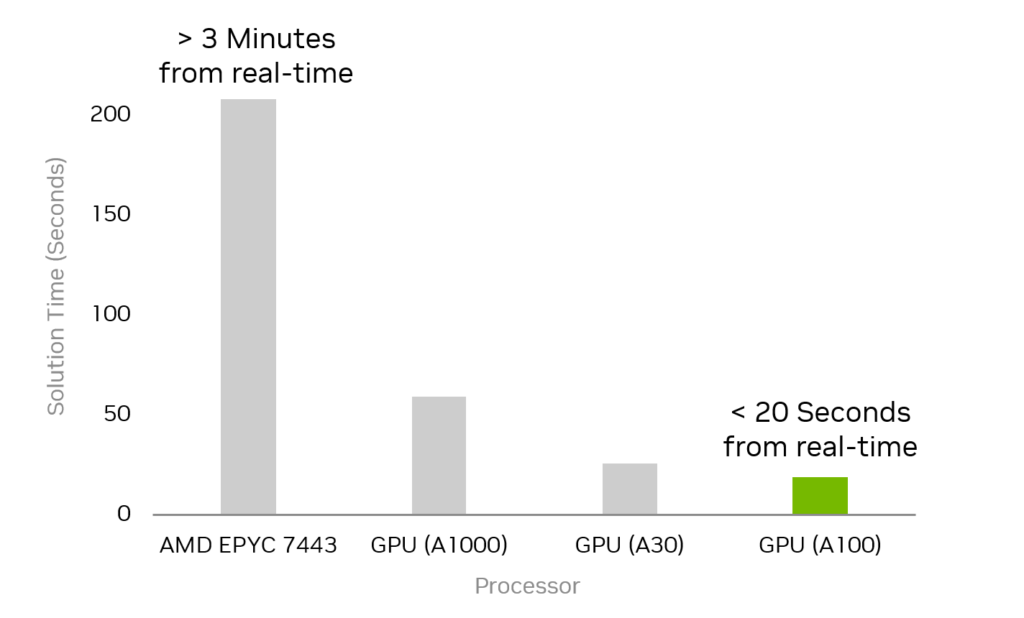
Their GPU-accelerated implementation resulted in more than a 10x speedup over the previous state-of-the-art implementation on an AMD EPYC 7443 CPU (Figure 3). The numerical factorization and triangular solve step was accelerated by a factor of 30x by replacing the CPU-based HSL MA27 linear solver with cuDSS.

These speedups were realized in part because the KKT procedures are particularly suited for cuDSS. They present a fixed sparsity pattern, ensuring the expensive and challenging to parallelize symbolic analysis step can be performed just one time in the preprocessing stage. Then, the rest of the algorithm relies only on the efficient cuDSS refactorization routine.

Redefining the limits of PSO with NVIDIA GH200

Some of the most important applications of PSO involve problems with much larger complexity, with problems writing with millions of variables and constraints. For example, the multi-period formulation helps predict future power demand and the security-constrained formulation helps ensure the reliability of national infrastructure with contingency planning.

The problems are so large and complex that they require breakthroughs in accelerated computing hardware to become tractable.

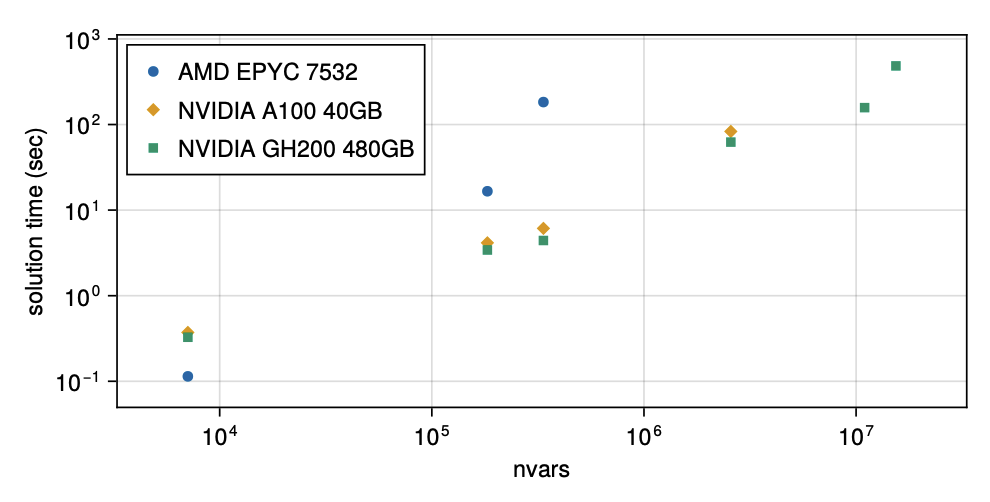
The NVIDIA Grace Hopper Superchip (GH200) enables MadNLP to solve problems that were previously considered intractable. A recent publication demonstrated how GH200 was necessary to solve a multi-period optimization problem with over 10M variables (Figure 4) and constraints thanks to 576 GB of unified memory (480-GB CPU plus 96-GB GPU).

For small problem instances, the CPU was faster, due to the overhead of data transfer to the GPU.

The results were groundbreaking enough for the authors to state, “We expect CPU/GPU systems with unified memory, like the NVIDIA GH200, will become mainstream hardware in the near future with even higher RAM capacities. These advances can provide powerful computational tools for electricity market operations.”

Accelerating next-generation energy efficiency

Sungho, François, and Alexis have already made immense strides towards the practical solution of challenging PSO problems. They plan to continue their work, improving the numerical precision and robustness of their solvers.

They are developing a new solver, MadNCL, which uses MadNLP to solve a series of subproblems that minimize an augmented Lagrangian. This approach shows great promise for improved accuracy and resilience to degeneracies in the optimization procedure.

These new approaches continue to rely on cuDSS and the rapidly evolving capabilities of NVIDIA GPUs, including the ability to scale to larger problems with multi-GPU multi-node support.

Get started with cuDSS

You can download the early-access cuDSS library to start accelerating your applications. For more information about cuDSS features, see NVIDIA cuDSS (Preview): A high-performance CUDA Library for Direct Sparse Solvers. For more information about other math libraries that can be used in conjunction with cuDSS, see CUDA-X GPU-Accelerated Libraries.

If you are interested in PSO and other GPU-accelerated nonlinear optimization applications, explore the ExaModels and MadNLP GitHub repos.

For a real-world deployment, find out how Honeywell integrated cuDSS into UniSim Design, achieving up to 78x performance improvement.

NVIDIA cuDSS Library Removes Barriers to Optimizing the US Power Grid